프로그래밍/알고리즘
코드업 2833
austag
2023. 3. 12. 21:04
이 글에선 코드업 2833문제를 해결해보겠습니다.
이 문제는 전에 올렸던 2832문제에서 변형하면 풀 수 있습니다.
문제는 다음과 같습니다.
OO이가 계단을 올라가려고 한다.
계단은 모두 n칸으로 구성되어 있다.
OO이는 한 번에 1칸, 2칸, 3칸을 오를 수 있다.
OO이가 k개 이하의 칸을 이용하면서 0번째 칸에서 출발하여 n번째 칸으로 올라가는 서로 다른 방법의 수를 구하는 프로그램을 작성하시오.
만약 n이 3이고, k가 3 이면
- 1 2 : 0번째, 1번째, 3번째 계단을 이용하여 목표에 도달
- 2 1 : 0번째, 2번째, 3번째 계단을 이용하여 목표에 도달
- 3 : 0번째, 3번째 계단을 이용하여 목표에 도달
으로 모두 3가지 경우가 있다.
입력
첫 번째 줄에 n과 k가 공백을 기준으로 입력된다.
[입력값의 정의역]
[1 ≤ n ≤ 40]
[1 ≤ k ≤ 15]
출력
계단을 올라가는 서로 다른 경로의 수를 출력한다.
1. 문제 분석
2832번과 다르게 이 문제는 3칸까지 오를 수 있습니다.
따라서 점화식은
f(n) = f(n-3) + f(n-2) + f(n-1)
입니다.
2. 알고리즘 설계

3. 코딩
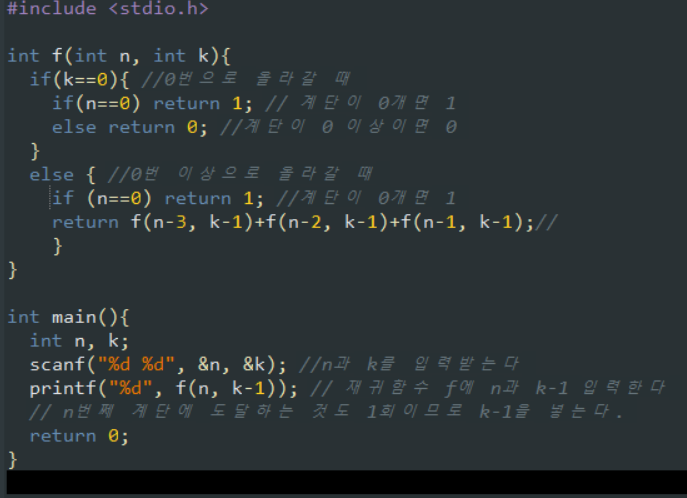
이렇게 n번째 계단을 k번 이하로 올라가고 한 번에 m개까지 올라갈 수 있는 문제를 변형하여 해결해 볼 수 있습니다.
이 유형의 문제의 점화식은
f(n) = f(n - m) + f(n - (m-1)) + ··· + f(n - 2) + f(n - 1)
임을 알 수 있었습니다.
코드업 2833