이번 글에서는 selection sort를 정리해봅시다.
Selection sort는 각 단계마다 가장 작은 key를 찾아서 적절한 위치에 넣는 정렬입니다.

위의 그림을 보면 각 단계별로 바뀌는 배열을 볼 수 있습니다. 매우 직관적인 방법이죠.
설명보단 바로 코드를 봐볼까요
void selectionSort(int list[], int n) {
cout << "< Selection Sort >" << endl;
for (int i=0; i<n-1; i++) {
// find minimum value
int min_index=i;
for (int j=i; j<n; j++) {
if (list[j] < list[min_index]) min_index = j;
}
// swap elements
cout << "Swap: " << list[min_index] << ", " << list[i] << endl;
int temp = list[i];
list[i] = list[min_index];
list[min_index] = temp;
for (int index=0; index<n; index++) cout << list[index] << " ";
cout << endl;
}
cout << endl << "sorted list: ";
for (int index=0; index<n; index++) cout << list[index] << " ";
cout << endl;
}
코드를 살펴봅시다.
1. 먼저 각 단계마다 배열에서 최소값을 구합니다.
for (int i=0; i<n-1; i++) {
// find minimum value
int min_index=i;
for (int j=i; j<n; j++) {
if (list[j] < list[min_index]) min_index = j;
}
2. 그리고 최소값이 들어갈 위치에 있는 값과 최소값을 교환합니다.
int temp = list[i];
list[i] = list[min_index];
list[min_index] = temp;
그럼 결과를 확인해 볼까요
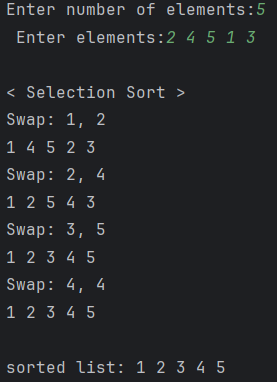
응용을 해보면 지금은 최소값부터 찾아 정렬했지만, 최대값부터 찾아 정렬할 수도 있습니다.
시간복잡도를 확인해보면 위에서 설명한 1번 코드에서 볼 수 있듯이
가장 좋은, 가장 나쁜, 평균적인 시간복잡도까지 $O(n^2)$ 임을 볼 수 있습니다.
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| [Sort] Bucket Sort (0) | 2025.04.24 |
|---|---|
| [Sort] Insertion Sort (0) | 2025.04.22 |
| [Sort] Bubble sort (0) | 2025.04.21 |
| [Sort] Intro (0) | 2025.04.17 |
| [천문] 월식 예측하기 (0) | 2023.10.25 |


