인공지능에 대해 공부하려고 [모두의 딥러닝] - 조태호 라는 책으로 공부를 하고 있는데 오늘은 선형회귀의 최소 제곱을 확인해 보려고 합니다.
먼저 딥러닝이라는 것은 무엇일까요?
인공지능이라는 범위에 '머신러닝'이 있고 그에 일부분에 '딥러닝'이 있습니다.

머신러닝 (machine learning) : 규칙을 일일이 프로그래밍하지 않아도 자동으로 데이터에서 규칙을 학습하는 알고리즘을 연구하는 분야
딥러닝 (Deep learning) : 인공 신경망을 기반으로 한 방법들
- 혼자 공부하는 머신러닝 + 딥러닝
딥러닝은 인간의 사고방식을 기반으로 한 컴퓨터의 학습 알고리즘입니다.
딥러닝의 가장 말단에서 이루어지는 기본적인 두 가지 계산 원리인 '선형회귀'와 '로지스틱 회귀' 가 있고
이 글에선 '선형회귀'를 공부한 내용을 다뤄보도록 하겠습니다.
선형회귀 (liner regression)는 변수 간 선형관계를 모델링하는 것이고 값을 예측할 수 있습니다.
예를 들어 '학생들의 중간고사 성적이 공부시간에 따라 다 다르다.'라는 것에서
독립적으로 변하는 값인 공부시간을 독립변수 x,
독립변수에 따라 종속적으로 변하는 중간고사 성적을 종속변수 y라 할 수 있습니다.
x가 1개면 '단순 선형 회귀', 2개 이상이면 '다중 선형 회귀'라고 합니다.
저는 이 선형회귀를 학교에서 한 화학실험 결과를 이용해서 구현해보도록 하겠습니다.
'기체의 종류와 상관없이 온도가 1℃ 올라갈 때마다 0℃ 때의 부피의 1/273씩 증가한다.' 라는 사를법칙을 통해 측정한 값으로 절대 0도를 구해보는 실험이었습니다.
이때의 독립변수는 온도, 종속변수는 부피라 할 수 있습니다.
이것은 단순 선형 회귀이고 y=ax+b 의 식으로 나타낼 수 있습니다.
(사를법칙의 공식이 있지만 공식을 모른다고 가정하고 얻은 결과값만 이용하여 식을 나타내어 절대영도 때의 부피와 온도에 따른 부피를 예측하겠습니다.)
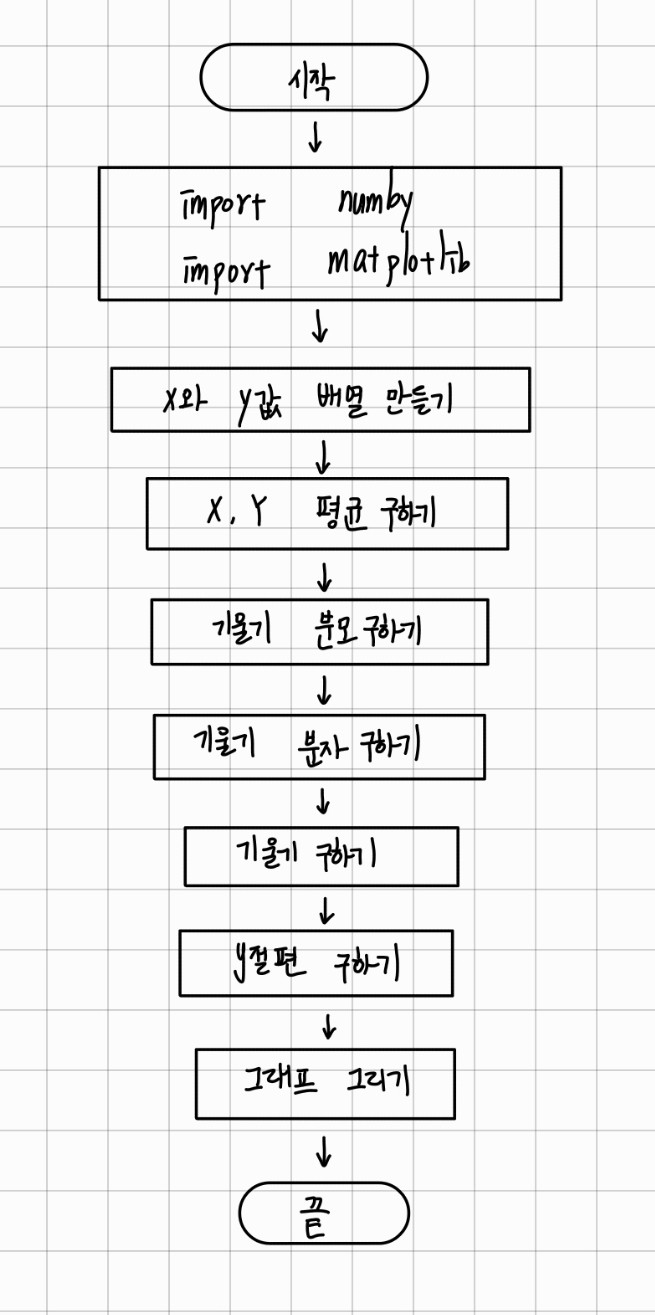
a, b의 값은 최소 제곱법이라는 공식을 사용하여 구할 수 있습니다.
기울기는 다음과 같이 구할 수 있고

y절편의 공식은 다음과 같습니다.

실험 측정값은 다음과 같습니다.
| 온도(℃) | 40.8 | 33.7 | 27.7 | 20.1 | 12.8 |
| 부피(㎤) | 4.312 | 4.235 | 4.1195 | 4.004 | 3.85 |
이제 파이썬으로 코딩해보겠습니다.
[ 코드 ]



이 식은 실험적 오차가 있기 때문에 정확하지 않습니다.
부피가 0일 때의 온도가 -220℃가 나왔기 때문에 실제 절대 영도인 -273℃와 약 -53℃의 오차가 있다는 것을 알 수 있습니다.
이렇게 선형회귀 중 단일 선형 회귀에서의 최소제곱법을 확인해 보았습니다.
[참고 서적: 모두의 딥러닝]
'프로그래밍 > 인공지능' 카테고리의 다른 글
| 오차 역전파와 활성화 함수 (0) | 2023.06.01 |
|---|---|
| 다중 분류(multi classification) (0) | 2023.05.31 |
| 퍼셉트론(Perceptron) (0) | 2023.05.30 |
| 로지스틱 회귀 (0) | 2023.05.17 |
| 경사하강법 (1) | 2023.05.16 |



